どーも、ききです。
今回は第二種電気工事士の筆記試験で出題される計算問題について解説していきます。
この筆記試験で、計算問題は全て捨てて受験される方は多いと聞いた事があります。
というのも全体で10問程度しか出題されず(全50問)6割以上で合格な為、計算問題以外(識別や法令、複線図など)でしっかり点が取れれば合格出来る為です。
適当に書いても25%で正解するので、運が良ければ多少点数を稼げます。
しかし、どうせ受けるなら少しでも万全で望みたいですよね。
受験した時に計算問題以外の問題が思ったより難しかったら元も子もないです(最近はやや難化傾向にあります)
逆に言えば計算問題で稼げるようになれば、少しでも有利に合格に近づくと思っています。
今回はみんなの苦手意識の強い計算問題を少しでも簡単に解く方法を伝授します。
今後受験される方の参考になれば幸いです。
何故計算問題は敬遠されるのか
何となく計算って聞くだけで苦手で嫌いって言う人多いと思います。

逆に好きって奴も中々いないと思うゾ…
第二種電気工事士の計算問題ではルートを使った問題が多数出てきます。
しかも電卓が使用不可なのでルート絡みの掛け算や割り算を自力で計算しなければいけません。

はい!この時点で無理!ありがとうございました
確かにまだ若い人ならまだしも、ある程度歳を取るともう掛け算とか自力でやるなんて考えたくもないですよね…
第二種電気工事士の計算問題は真面目に解こうとすると結構時間が掛かる問題もあります。
しかし、過去問を見ているとほとんど同じような問題の繰り返しで、ある程度パターンを覚えてしまうとパッと見ただけで答えが分かるようになります。
他の項目は暗記勝負ですが、こちらの計算問題もはっきりいって暗記です。
すなわち余計な計算をしなくても、パターンを覚えるだけである程度点が取れるようなものもあります(答えを暗記する訳ではありません)
全く計算しない訳ではありませんが、極力無駄な計算はしないようにして少しでも負担を減らす事だけを考えてこちらの記事を書いています。
この記事を読み終える頃には、もしかしたら計算問題が好きになってる…かもしれません(ない
大前提に覚えなければいけない公式、数値
公式を暗記しておくだけで解ける問題やその公式自体が答えになっている問題もあります。少しでも覚えやすいように工夫していくので頑張って覚えていきましょう。
合成抵抗の問題
- 直列接続はそれぞれ足すだけ
- 並列接続は和分の積
- 直列は分圧、並列は分流
- 電流は抵抗の小さい方に流れる
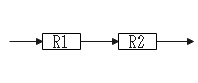
直列はそのまま足すだけです(R1+R2)
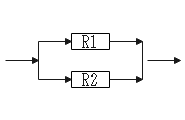
並列は各抵抗を足したものを掛けたもので割ります。((R1×R2)÷(R1+R2))
直列回路は分圧で並列回路は分流になるとだけ覚えておいて下さい。同じ抵抗が直列に並んでいたら半分になります。
オームの法則、抵抗率
- 電圧(V)=抵抗(R)×電流(A)
- 電気抵抗は長さに比例、断面積に反比例、直径または半径には1/4になる
オームの法則はこのV=RIだけ覚えておけば問題ありません。求めたい部分を変換すれば電圧、電流、抵抗全て求める事が出来ます。
抵抗率の公式は
電気抵抗R=ρ(抵抗率)xℓ(長さ)÷A(断面積)
です。こちらについては過去問題解説の記事で詳しく解説しましょう。
熱量と電力量
- 熱量H(J)=電流I2x抵抗Rx時間t秒
- 電力P(W)=電圧Vx電流I
- 電力量W(W・s)=電力Px時間t秒
- すなわち電力量=熱量
この公式以外に1時間は3,600秒と覚えておきましょう。
少しごちゃごちゃして見えますが、
H=I2xRxt (IxR=V)なので、H=VxIxt H=W
と、結局同じ式になると覚えておくといいです。
交流電圧、位相差
- 実効値=最大値÷√2
- コイルは90℃位相が遅れる
- コンデンサは90℃位相が進む
問題用紙の冒頭にはたいてい
「本問題の計算で√2、√3及び円周率πを使用する場合の数値は次によること。 √2=1.41、√3=1.73、π=3.14」
などと書かれていますので、計算問題を解く時はこの数字に当てはめて計算しなければいけません。
これらの数字を使う際には√2=1.5、√3=1.7、π=3と簡略化します。
単相交流
- 直列回路の全体の抵抗(インピーダンス)のうちコイルの部分を除いた所に掛かる電力を有効電力
- 力率cosθ=有効電力÷皮相電力
- コンデンサを使用して力率の改善をした場合電流は減少する
簡単に説明すると、直列回路で抵抗とコイルが混在している場合、全体の抵抗からコイル部分を除いて求めるという事です。
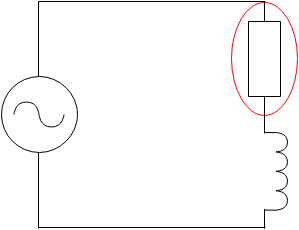
このような回路の場合、赤丸で囲った部分に有効電力が掛かります
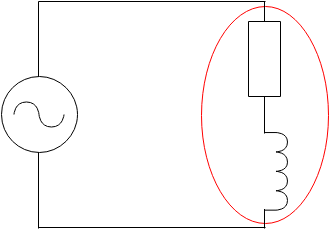
全体的に掛かる電力(赤丸で囲っている部分)は皮相電力という
有効電力を求める場合、全体のうち上の抵抗分を問題では求める事になります。ちなみに、コイル側だけに掛かる電力は無効電力と言いますが、あまり気にしなくても大丈夫です。
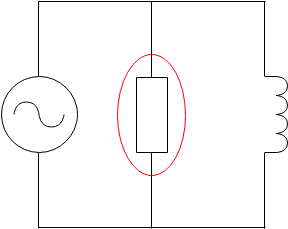
並列回路でこのような配置の場合、やはりコイル側は無効電力となるので赤丸で囲っている部分のみの有効電力を求めればいいです。
この全体の抵抗値をインピーダンスと呼び、求め方は
√抵抗値2+コイル側の抵抗値2となります。
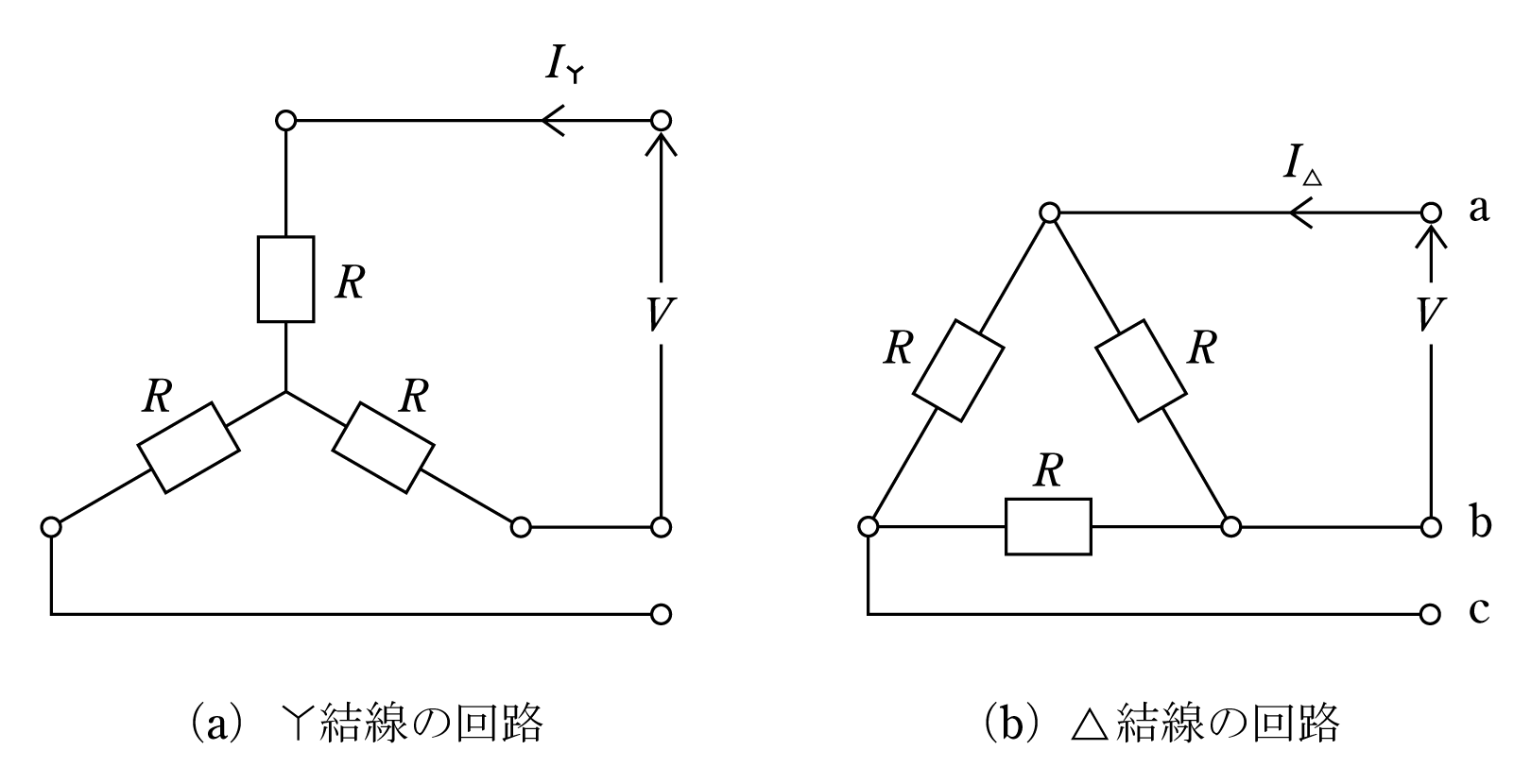
三相交流回路
- Y結線…線間電圧=√3x相電圧、線電流=相電流
- Δ結線…線間電圧=相電圧、線電流=√3x相電流
- 三相電力=3x相電圧x相電流x力率=√3x線間電圧x線電流x力率
- 三相交流の電力は各相の電力の和(P=P1+P+P3)
式がたくさん出てきますが、Y結線は電圧に√3,Δ結線は電流に√3とだけ覚えておきます。この二種類の回路は大抵試験に出てくるので、押さえておきましょう。
引用:日本電気技術者協会-Y結線とΔ結線の回路-
電圧降下と電力損失
- 単相2線式の電圧降下=2rI、電力損失=2rI2
- 単相3線式の電圧降下=rI、電力損失=2rI2
- 三相3線式の電圧降下=√3rI、電力損失=3rI2
- 単相3線式の中性線電流は、平衡負荷の状態では0A
これは全て丸暗記する価値があります。なぜなら、この公式自体が答えになる問題が出てくる可能性があるからです。
絶縁電線の許容電流
こちらからは数字を暗記していきます。過去問を解きながら少しずつ覚えていくといいでしょう。
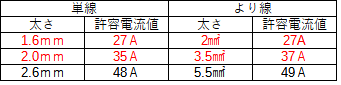
特に赤字は良く出題されますが、数値が大きいものもそれなりに出るので一通り覚えておきましょう。
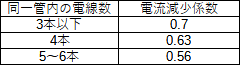
こちらの数値は問題文に記載されている事が多いですが、もし記載されていないと求める事が出来ないので一応覚えておくと安心です。0.7から0.07ずつ減っていくと覚えておきましょう。
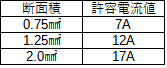
コードの許容電流を求める問題もたまに出てきます。念のため押さえておけば出てきた時にすぐ答えが出せます。
過電流遮断器に定められた動作時間

屋内幹線の許容電流

IMは電動機の合計で、IHは電動機以外の合計です(IWは許容電流)Mの合計がM以外の合計より大きいか小さいかで解き方が変わってきます。
分岐回路
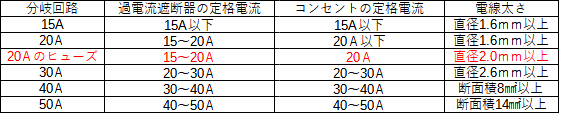
この表の20Aのヒューズはあまり試験には出てこないですが、赤色にしてあるのは
20Aのヒューズを拠点に定格電流と電線太さが比例して変わる。つまり、30Aになれば定格電流と電線太さは大きくなり、15Aになれば小さくなるという事を示しています。
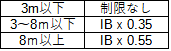
これは分岐回路の開閉器及び過電流遮断器の施設位置の問題で問われる数字で、とりあえず問題の長さを表の数字に当てはめて計算するだけです。8m以下は0.35とそれ以上は0.55とだけ覚えておきましょう。
とりあえず、覚える事はここまでで終わりです。
ここまでの内容を一気に覚えるよりも過去問を解きながら少しずつ覚えていけば効率良く覚える事が出来ると思います。
過去問解説
いよいよ過去問の解説に入ります。
比較的良く出ている問題を抜粋しています。
ではいきましょう。
過去問はこちらのサイト様から引用させて貰いました。
過去問自体は「電気技術者試験センター」のサイトに掲載されています。
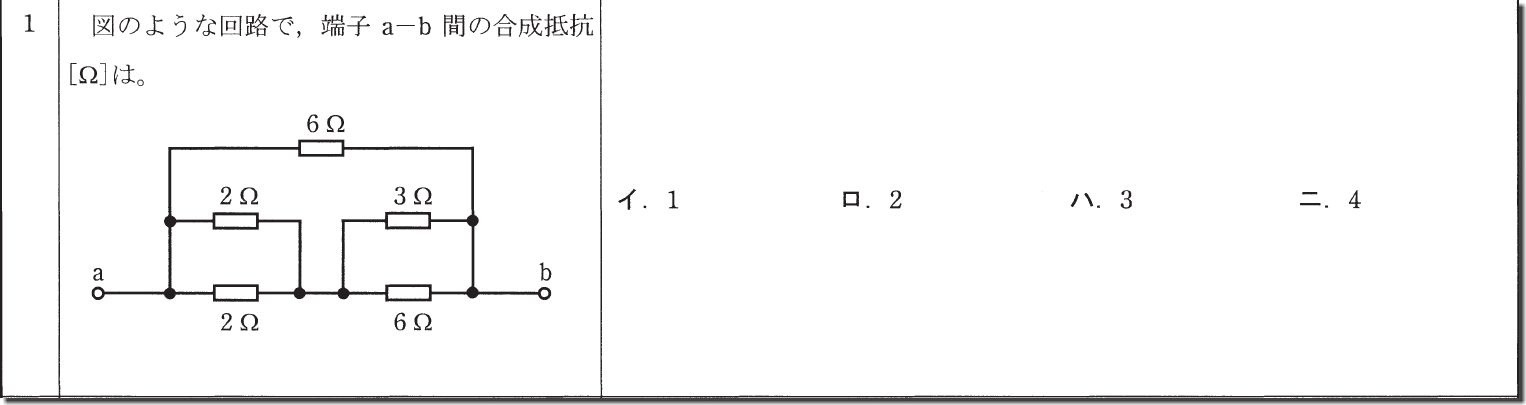
合成抵抗の問題はこのようなパターンが多いです。
一見難しそうに感じますが、直列と並行の合成抵抗計算の解き方で解けます。
まず、左下の2Ωと2Ωが並列に繋がっている箇所がありますが、こちらを並行回路の求め方で求めると
(2Ω×2Ω)÷(2Ω+2Ω)=4÷4=1
となります。
次に右側の3Ωと6Ωも同じように求めると
(3×6)÷(3+6)=18÷9=2Ω
この二つを求めると、左側と右側で直接回路になるのでそのまま足します。
1+2=3Ω
そして、今求めた3Ωと上の6Ωが並列回路になっているので、同じように求めますが、実はこれ右側の合成抵抗を求める式と全く同じ式になります。
すなわちそれが答えとなり、解答は「ロ」となります。
…
どうですか?意外と簡単でしょう?(え
割と簡単目な計算問題で解き方さえ分かれば怖くありません。
このように解き方さえ分かればほとんど解けるので、捨てるなんて勿体ないです。
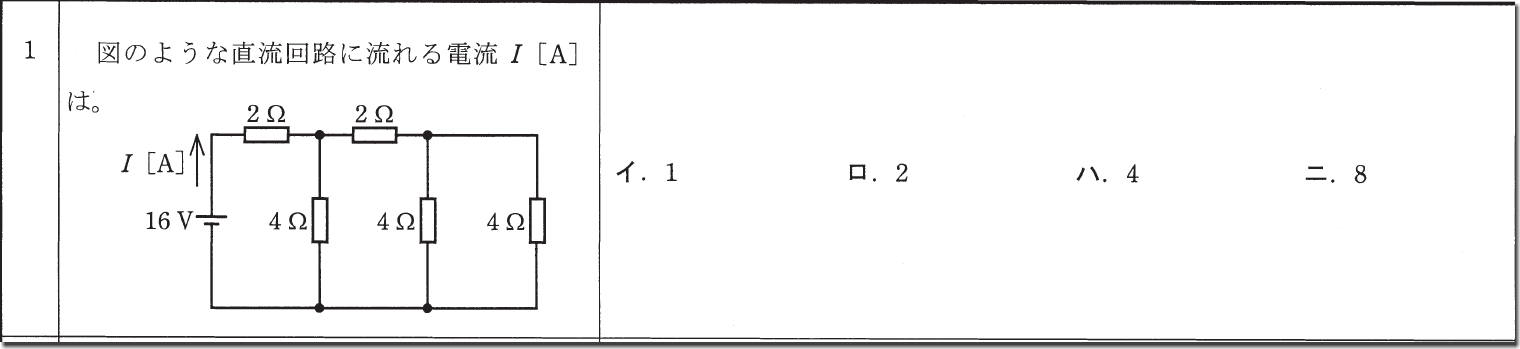
この問題も同じように合成抵抗を求めていきます。
まず、右側の4Ωと4Ωを並列回路で求めると
(4×4)÷(4+4)=2Ω
次にそのすぐ左上の抵抗2Ωと今度は直列になるので、足します。
2+2=4
で、その横の4Ωとまた並列となるので求めます。
(4×4)÷(4+4)=2Ω
再びその左上の抵抗と直列になるので、足します。
2+2=4Ω
これが合成抵抗となります(結局同じ計算繰り返してるだけ…)
次に電流を求めますが、こちらの公式は
V=RI(ブリ)
でしたよね?(覚えてない
V=16なので、
16=I×4、I=4
となり、答えは「ハ」となります。
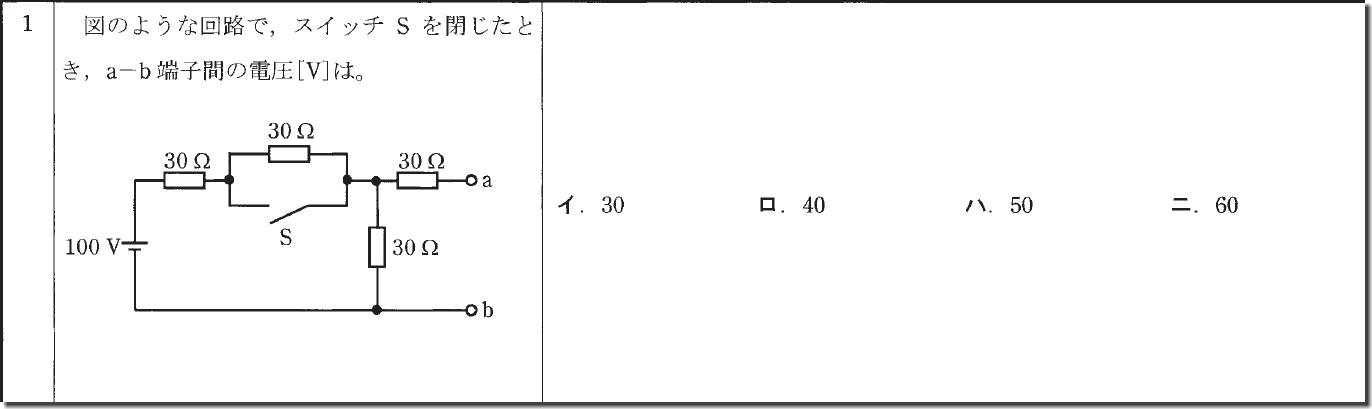
まず、このスイッチSを閉じると、抵抗は小さい方に流れるので閉じた方は抵抗がない為、こちらに電流が流れます。
次にaの横の30Ωですが、aの地点のように途切れている回路には電流が流れません。
この2点を考慮すると、スイッチSの上の30Ωとaの横の30Ωは無視出来ます(ここ重要)
そして、残った30Ωが2つ直列に繋がった状態で残ります。
ここで、分圧という言葉が出てきますが、純粋に全体の電圧を各抵抗(今回は同じ抵抗値)で分散するだけなので、計算は
100÷2=50
となり、答えは「ハ」となります。

抵抗値の所で長さに比例して直径に反比例する~なんたらかんたらって説明しましたが、それ以前に「イ」の「温度が上昇すると大きくなる」の文面が間違っていると余計な事を考えずに覚えておけば解けます。
この問題はいつも温度が上昇するって選択肢が出てきますが、それが間違っているのでこれは答えをそのまま覚えましょう。
って事で答えは「イ」です。

先程の問題と違ってこちらでは抵抗値の公式を使って求めていきます。
が!!
絶縁電線の許容電流の表を暗記していれば、計算する必要ありません。

これです。
問題の直径2.6mmはこの表の単線の太さに該当します(線の太さなので)
この表では48Aとなっています。
そして、選択肢の断面積5.5㎟はより線の太さに該当します。
この表では49Aとなっています。
問題では「抵抗値が最も近い」とあるので、全く同じ数字でなくても問題ありません。
つまり、答えは「ニ」となります。
※この問題も公式に当てはめて解く事も可能ですが、余計な計算はしない方向でいきましょう。
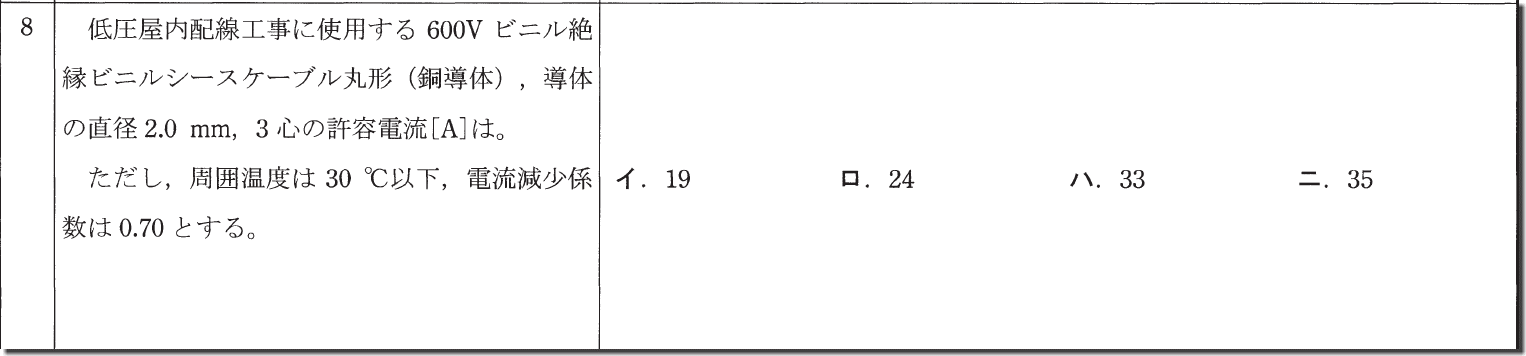
この問題も先程の表を暗記していればすんなり解けます。
まず、直径2.0mmとあるので、表では35Aとあります。
純粋にこの数字に電流減少係数を掛ければ答えが出ます。
そして、実際に掛けて計算すると
35×0.7
となります。
…
ちょっと0.7なのでまだマシですが正直計算が面倒ですよね?
なので、消去法で解いていきます。
まず、35に0.7を掛けているので「二」の35はありえません。
次に35の半分は17.5ですよね?あとは35を10等分すると3.5ですよね?
ならあとは足すだけです。
17.5+3.5+3.5=24.5(0.5+0.1+0.1と考えます)
となりまだ比較的計算はしやすくなったかと思います。
って訳で答えは「ロ」です。
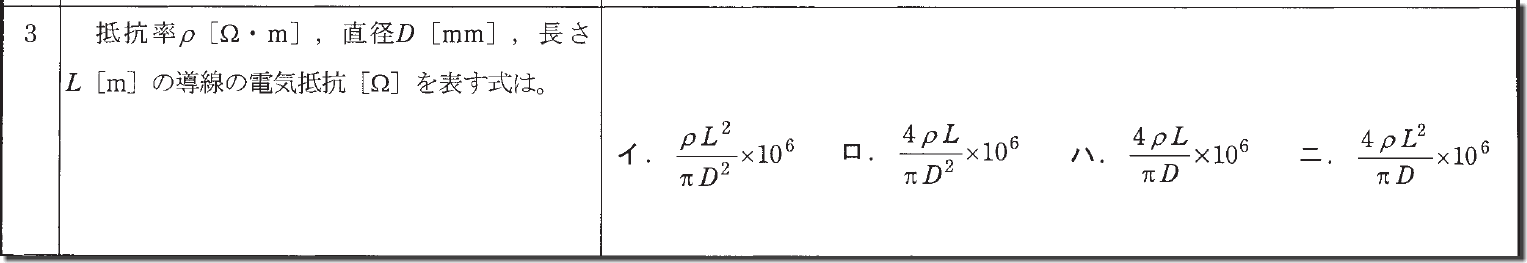
電気抵抗の問題でこのような問題も出てきますが、ちょっと真面目に計算するのは面倒なので、この問題は「ロ」の形を覚えておきましょう。
覚えるポイントはパッと見た時に4とD2が入っている式が正解です。

熱量のこの問題は、まず、全ての数字を掛けます。
60×20×4.2=5,040
そして、問題文に必要な電力量(kW/h)とあるので、これを秒で割ります(3,600秒)
5,040÷3,600=1.4
よって答えは「ハ」となります。
…

ちょっとこれ計算面倒だけど、簡単にならないの?
えー、まず5040を5000、3600を3500にしてみます。
5000÷3500
更に約分して
50÷35
大分楽になりましたね。これも答えは約1.4となります。

こちらはこの公式を使います。
・H=I2×R×t
そして、1時間は3,600秒なので、
15×15×0.2×3,600=162,000
となり、求める熱量が「kJ」なので、これを1,000で割ります。
162,000÷1,000=162
よって「ニ」となります。
これが正式な解き方ですが、少し楽しましょう。
大前提に最後に1,000で割った事を覚えておいて下さい。
まず、 15×15×0.2×3,600=162,000 の15×0.2を先に計算すると「3」になります。
なので
3×15×3600
となって
45×3,600
になります。
この時点で1,000で3,600を割ってみましょう。すると
45×3.6
となります。
大分簡単になったと思いますが、45の3倍でパッと見100以上の数字と分かると思います。
そして、選択肢を見ると「ニ」以外100を超えていないので、必然的に答えは「二」となります。

この問題は
・実効値=最大値÷√2
この公式を使います。
最大値は148と分かっているので
実効値=148÷√2
となります。
前の項目で√2は1.5として計算しましょう、と伝えましたがこれに当てはめると
148÷1.5
更に148を150にすると
150÷1.5
と大分求めやすくなりました。
でこれを求めると100になるので、一番近い「ロ」が答えとなります。
まぁ、パッと見「ハ」と「ニ」は選択肢から消えるので、答えを出す前に選択肢を消去する事をまずは考えましょう。
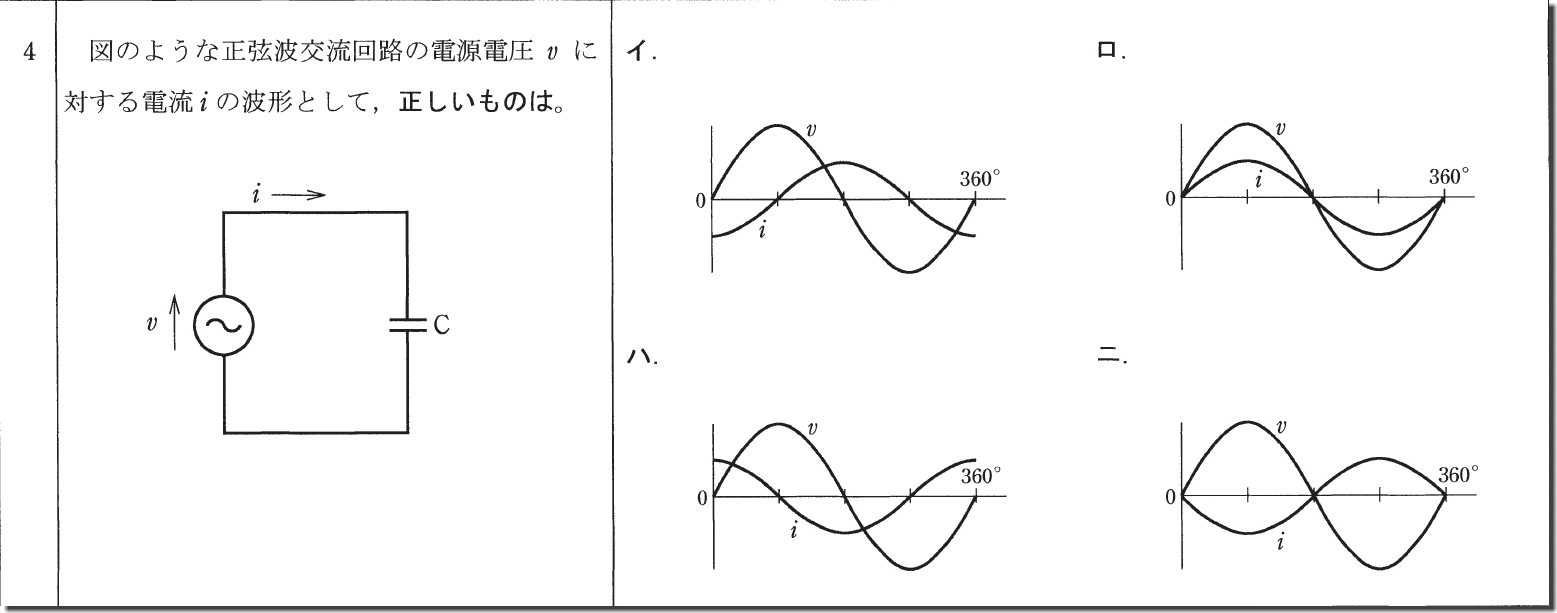
これは
・コンデンサは90℃進む、コイルは90℃遅れる
これを参考に解いていきます。
図のCの部分の二本線みたいな奴はコンデンサで波打っている奴がコイルです(次の問題の問題の16Ωの部分です)
これは最低限押さえておきましょう。
90℃遅れるとか進むっていうのは、右側のグラフの0の地点から上か下かで答えを出します。
良く分からなければ、形で覚えましょう。
答えは「ハ」となります。
※ちなみにコイルの場合「イ」になります。最悪分からない時も0から始まらないという事を頭の片隅に入れておけば「イ」と「ハ」の二択まで絞れます。
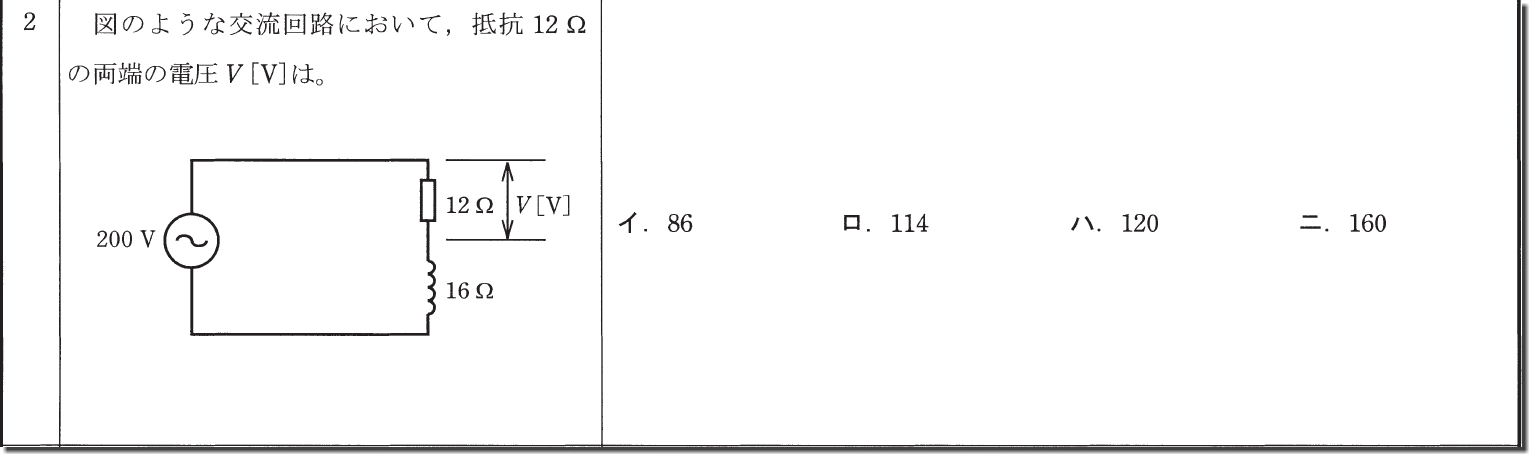
えー、この記事で一番伝えたかった問題はこれです。
この問題まともに計算するとインピーダンスを求めて…っとかなり面倒なんですが、簡単に解く方法があります。
ちょっと難しい話をすると、電気工事士のこの手の問題は「三平方の定理」で当てはまる問題が多いです。
三平方の定理についての解説はこちらではしませんが、知りたい方は自分でググって下さい(丸投げ
まず、3:4:5という数字を覚えておきます。
そして、全体の電圧が200V、求めたい部分の抵抗が12Ω…つまり、3:4:5の3が12Ω、コイル部分が4で16Ω、5が全体の20Ω(200V)と考えます。
比率が5で200なら3は120ですよね?なので答えは「ハ」となります。
余計な事は考えなくてもいいです。パッと問題を見た時に求めたい部分の比率を確かめれば計算せずに一瞬で答えが出ます(ちなみにコイル側は160V)
電気工事士の問題ではほぼこの3:4:5の比率ばかり出題されます。
このインピーダンスの解き方は他の問題でも活躍するのでしっかり覚えておいて下さい。
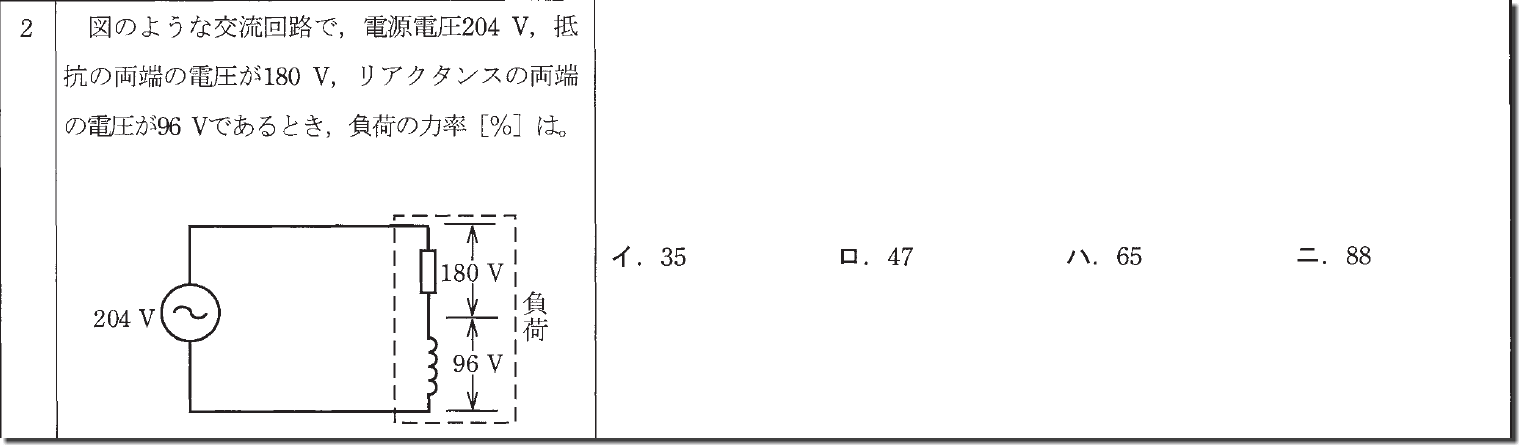
力率は図の180Vの部分の比率なので、純粋に全体のうちの180Vを求めれば答えが出ます。
180÷204=約88%
その時点で答えは「ニ」しかありません。
ちょっと面倒なので、少し数字を簡単にします。
180÷200
更に約分して
18÷20
これは0.9となり答えの0.88と近いので「二」となります。

この問題はまともに計算すると非常に面倒なので、この問題も「ロ」の形を覚えてしまいましょう。
ポイントは100Rと√と覚えましょう。

コンデンサを設置すると改善されるという事は、無駄な電力を消費しなくなるという事なので答えは「二」となります。

この問題も余計な計算をせずに答えは「ロ」の5と覚えましょう。
この問題の公式はI=V÷2πfLという公式を使って解きますが、面倒なので50Hzは6A、60Hzは5Aと覚えてしまいましょう。大体同じ数字で出題されます(もし数字が違ったらごめんなさい
計算しても正直難しくはないですが、余計な手間は省きます。
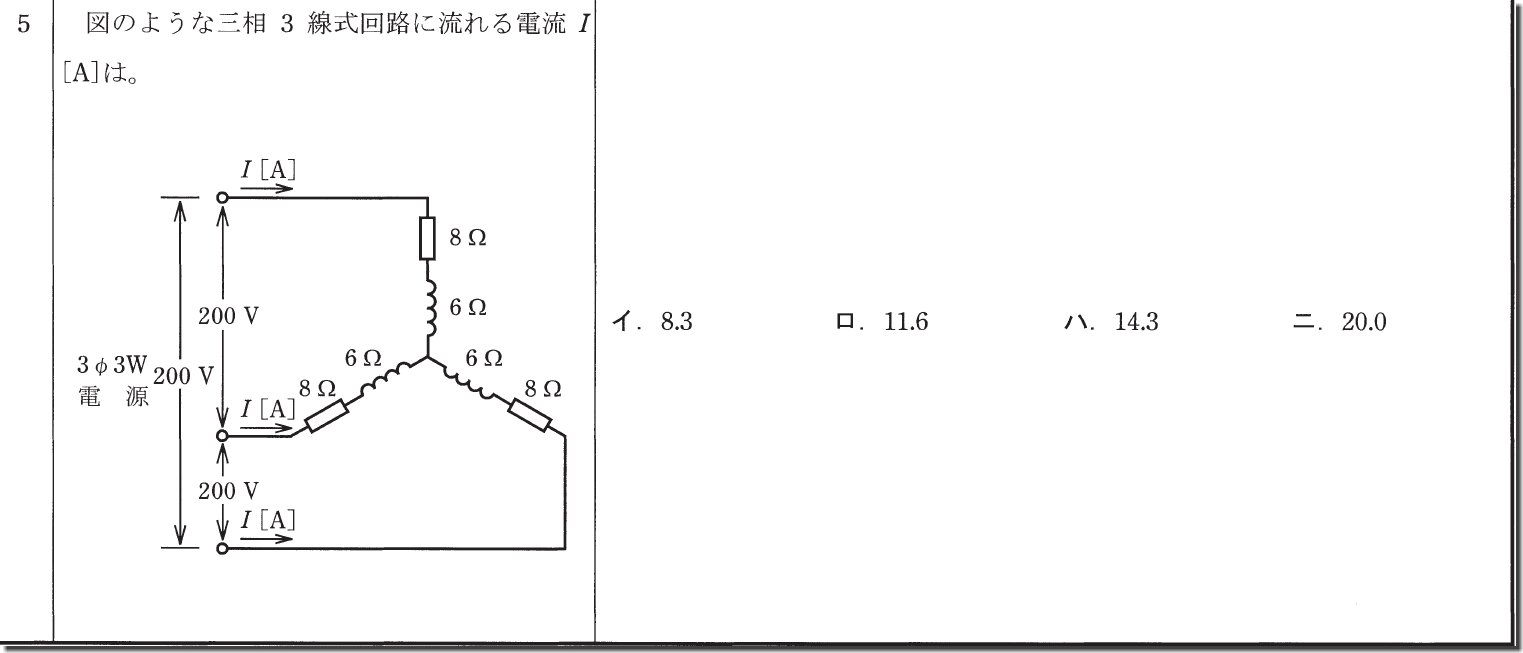
ここから三相交流の問題に入ります。
一見難しそうに感じますが、少しでも楽して解けるように解説していきます。
Y結線は、
線間電圧=√3×相電圧、線電流=相電流
でしたよね?(忘れた
まず、相電圧を求めます。
相電圧=200÷√3
ちょっと計算が面倒なのでちょっと置いておきます。
まず、抵抗のインピーダンスは先程の三平方の定理で10Ωと分かります。
そしてI=V÷Rなので
(200÷√3)÷10
これで答えが出ますが、√3は1.7なので2と1の間…200÷2=100、200÷1=200なのでその間だと分かります。
次に10で割るので20から10の間と分かります。
この時点で「イ」と「二」は消去出来ます。
ここで
20÷1.7(√3は1.7として計算)
これだけ頑張って計算します。すると11.7となり近い数字は11.6です。
よって答えは「ロ」です。
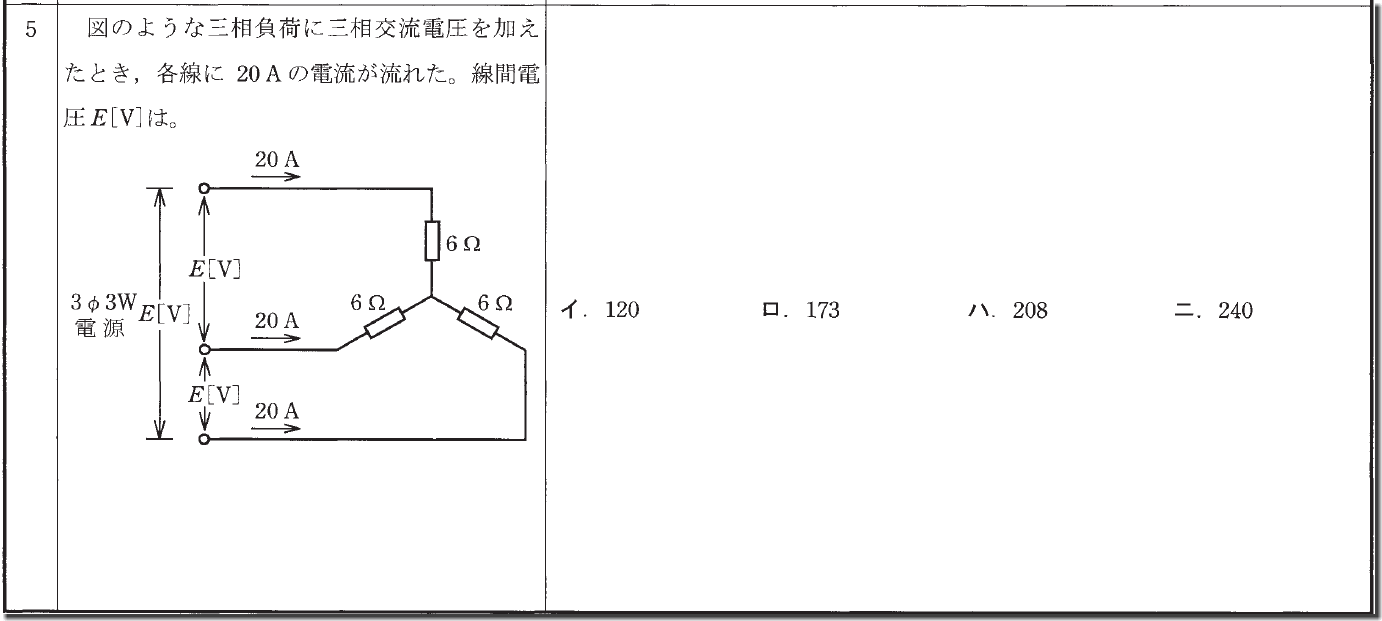
この問題はまず線間電圧を求めます。
20×6=120V
あとはこれに√3を掛けるだけです。
解く前にまず「イ」と「二」は消去出来ます。
120に1.5倍で180なので、1.7倍は180以上です。
よって答えは「ハ」です。
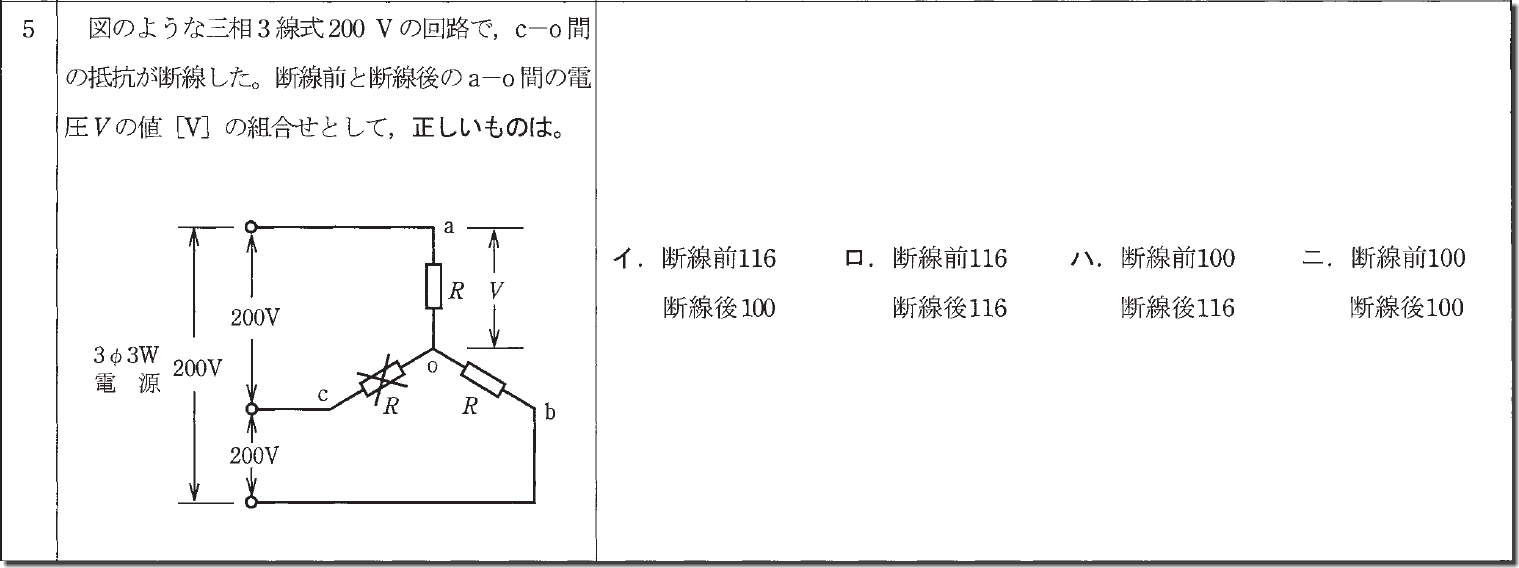
この問題は前に解説した直列回路の分圧を使用します。
断線するとa-o-bと普通の直列回路になります。
そしてRが二つあり、分圧されるので純粋に
200÷2=100
これが断線後の電圧です。
この時点で「ロ」と「ハ」は選択肢から消えます。
次に断線前は普通に相電圧を求める公式で
200÷√3
ですが、これを求めるまでもなく「ニ」は両方100なので不正解。
と言うことで正解は「イ」となります。
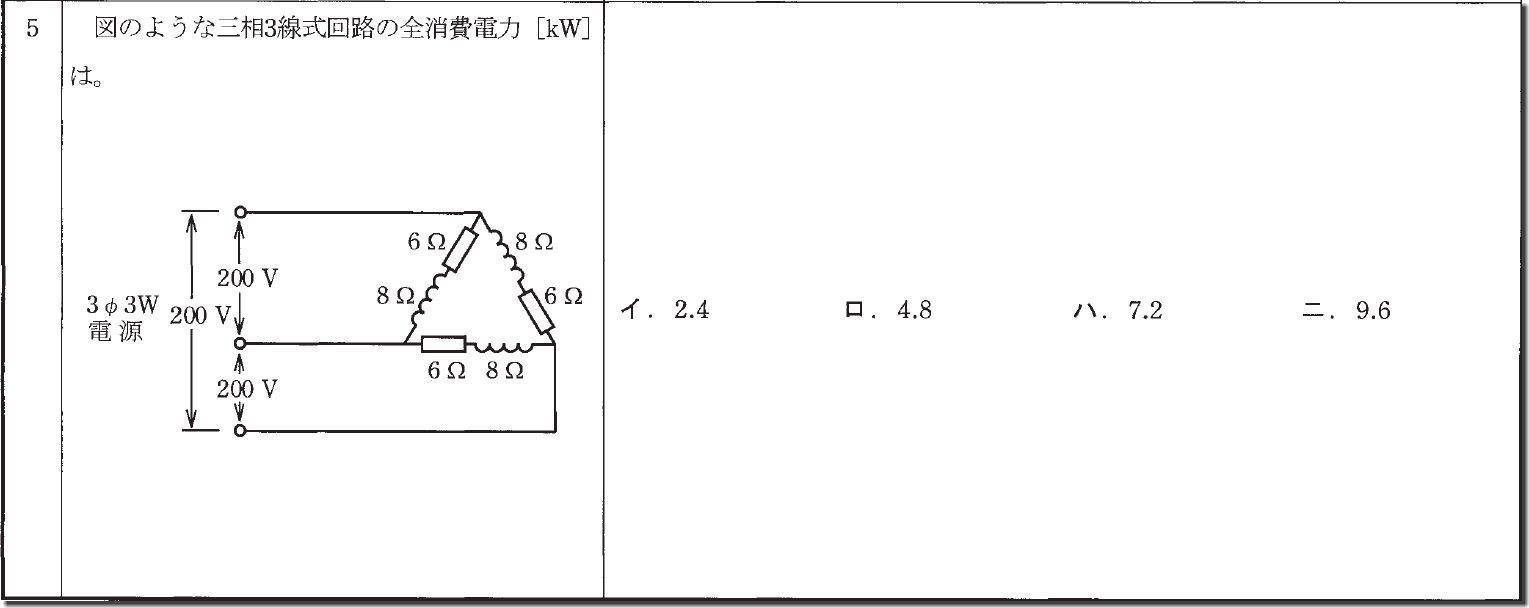
次はΔ結線です。こちらは
・線間電圧=相電圧、線電流=相電流×√3
でしたよね?ん?
しっかり覚えましょうね。
まず電流を求めますが、電圧は線間電圧=相電圧で、抵抗はやはりこの比率(3:4:5)なのでインピーダンスは10Ωです。
電流=200÷10=20A
力率側の抵抗は6Ω、電力の公式はP=I^2×Rなので
20×20×6=2400
でこれが3本あるので3倍して7,200。
「kW」とあるので1,000で割って7.2
つまり答えは「ハ」となります。
ハハハッ(黙れ
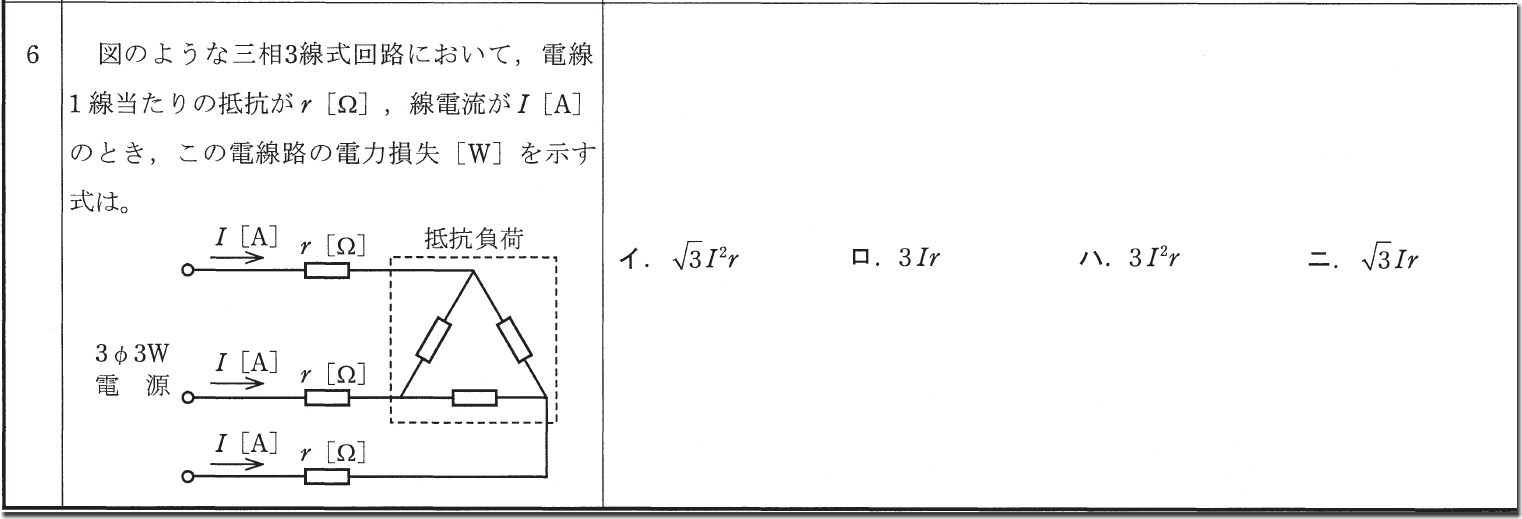
この問題は電力損失の式がそのまま答えになっています。
なので、公式を覚えているだけで点が取れる、ある意味サービス問題です。
三相三線式の電力損失は3I2rでしたよね。
答えは「ハ」です。
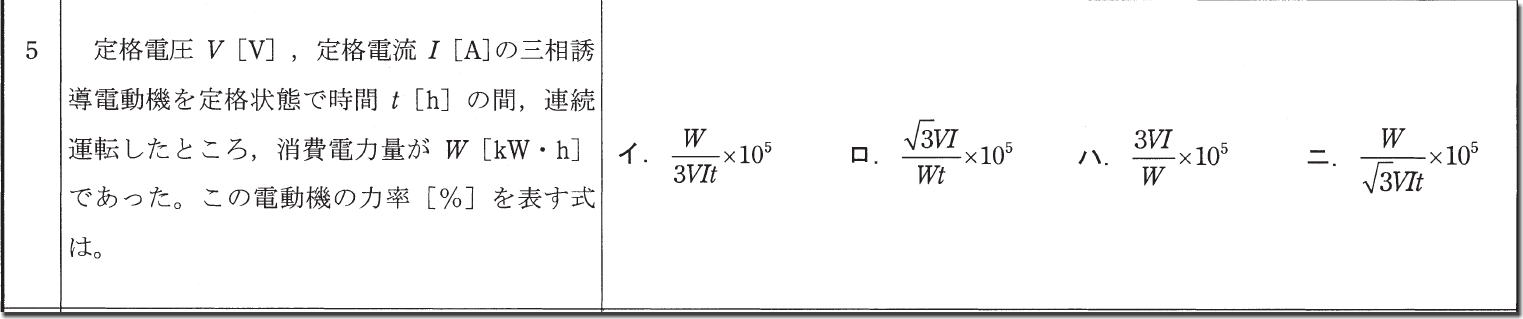
この問題も普通に解くと面倒なので、そのまま答えを覚えましょう。
答えは「二」です。
分母に√があると覚えておきましょう。
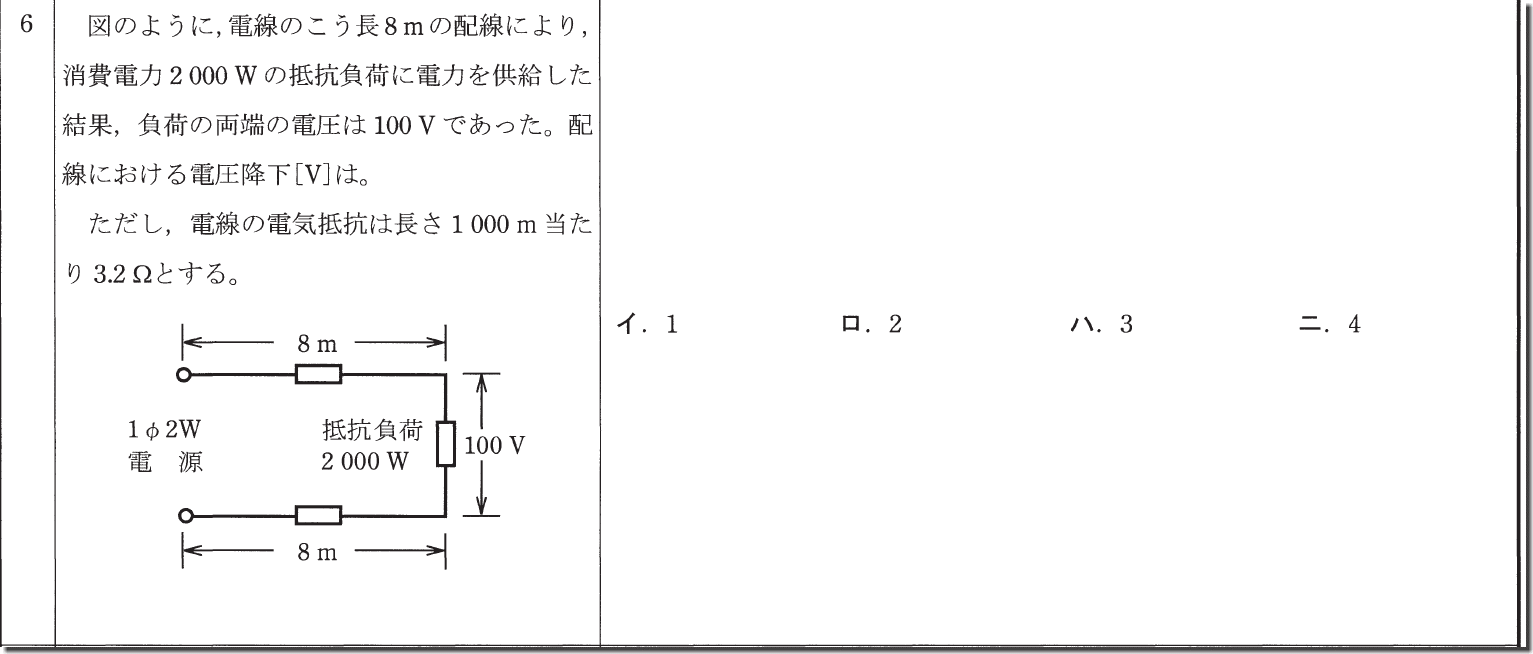
この問題はまず、電流を求めます。W=I×Vなので
I=2000÷100=20
そして抵抗は1000m当たり3.2Ωなので、1mは
3.2÷1000=0.0032
その8倍なので
0.0032×8=0.0256
これを、単相二線式の電圧降下の式に当てはめます。2Irでしたよね。
2×20×0.0256=1.024
なので答えは「イ」となります。
…
ちょっと抵抗の計算が面倒なので、少数とか抜きにして純粋に32×8で計算しましょう。
そーすると32×8=256になります。最後に10000で割るようにします。
同じように公式に当てはめると
2×20×256
となります。そして
40×256
ぱっと見10000前後って分かると思いますが、それを10000で割ると1付近しかないので答えは「イ」ですね。
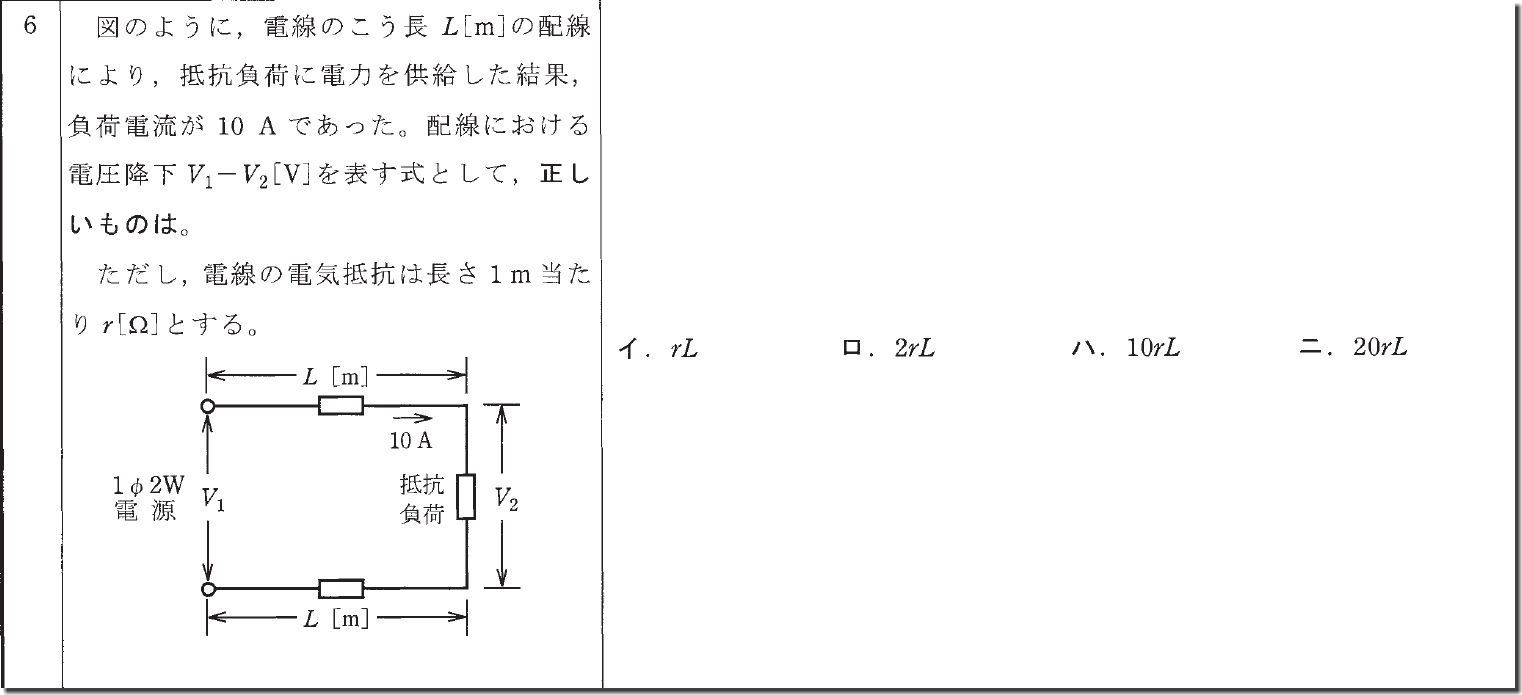
これも公式が分かれば一瞬で答えが分かります。
まず、単相二線式の電圧降下は2Irでしたよね。
I=10Aなので2×10×r
1m当たり「r」なので、L(m)は純粋に掛けたLr
それぞれ合体して20Lr。答えは「二」ですね。
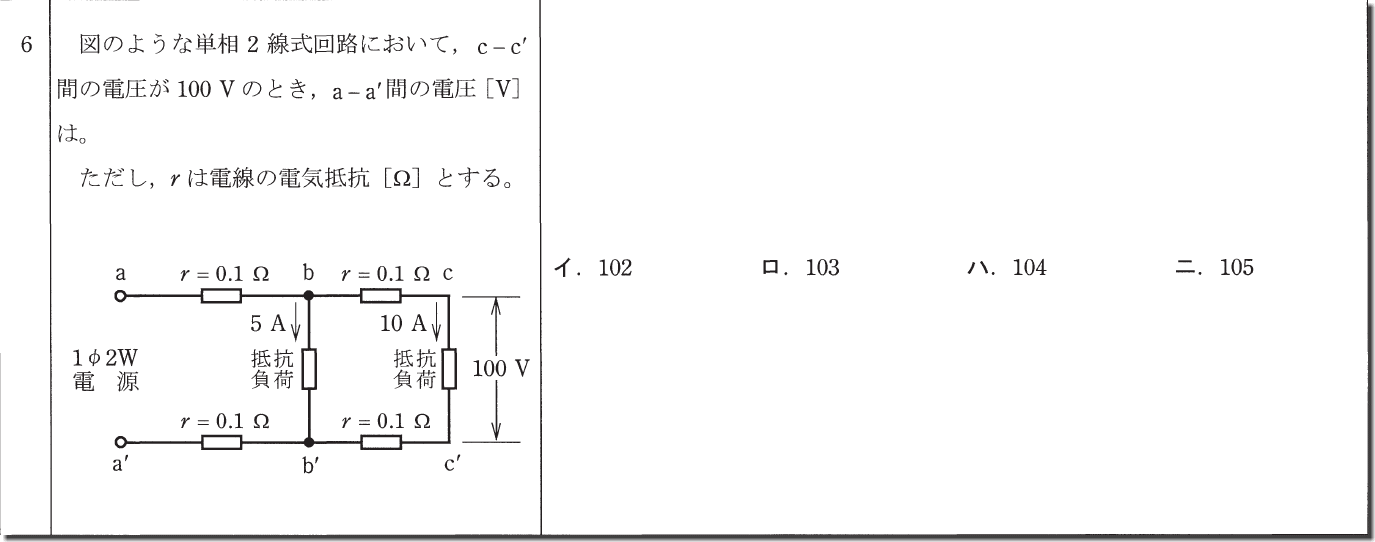
この問題は右側と左側を別々に計算します。
まず、bc間の電圧は普通にV=Irで求めます。
V=10×0.1=1
でそれが上と下(bcとb’c’)あるので純粋に2倍の2。
次にab間は一見5Aですが、右側の10Aを足したものが元々の電流値なので足して15A
同じように計算して
V=15×0.1=1.5
でこれも2本あるので1.5×2=3
そしてこれらを全て足したものとcc’間の電圧を足したものがaa’間の電圧となり、答えとなります。
2+3=5、100+5=105V
よって答えは「ニ」です。

単相三線式の電圧降下はIrなので
10×.01=1
でこのab間の電圧は105Vですが、これから電圧降下分を引いたものが答えとなります。
105-1=104
よって答えは「ハ」です。
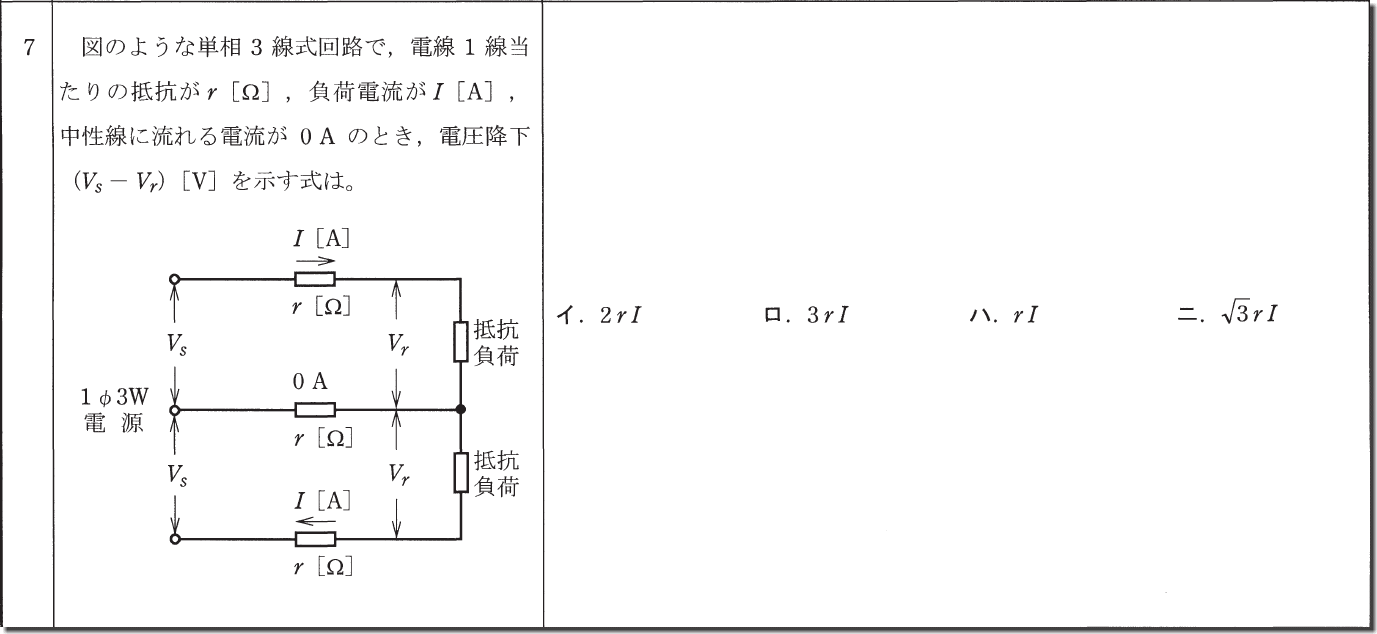
これもさっきの問題で使用した単相三線式の電圧降下の公式Irがそのまま答えとなります。
他の問題でもありましたが、公式がそのまま答えになる問題もたまに出題されるのでしっかり覚えておきましょう。
答えは「ハ」です。
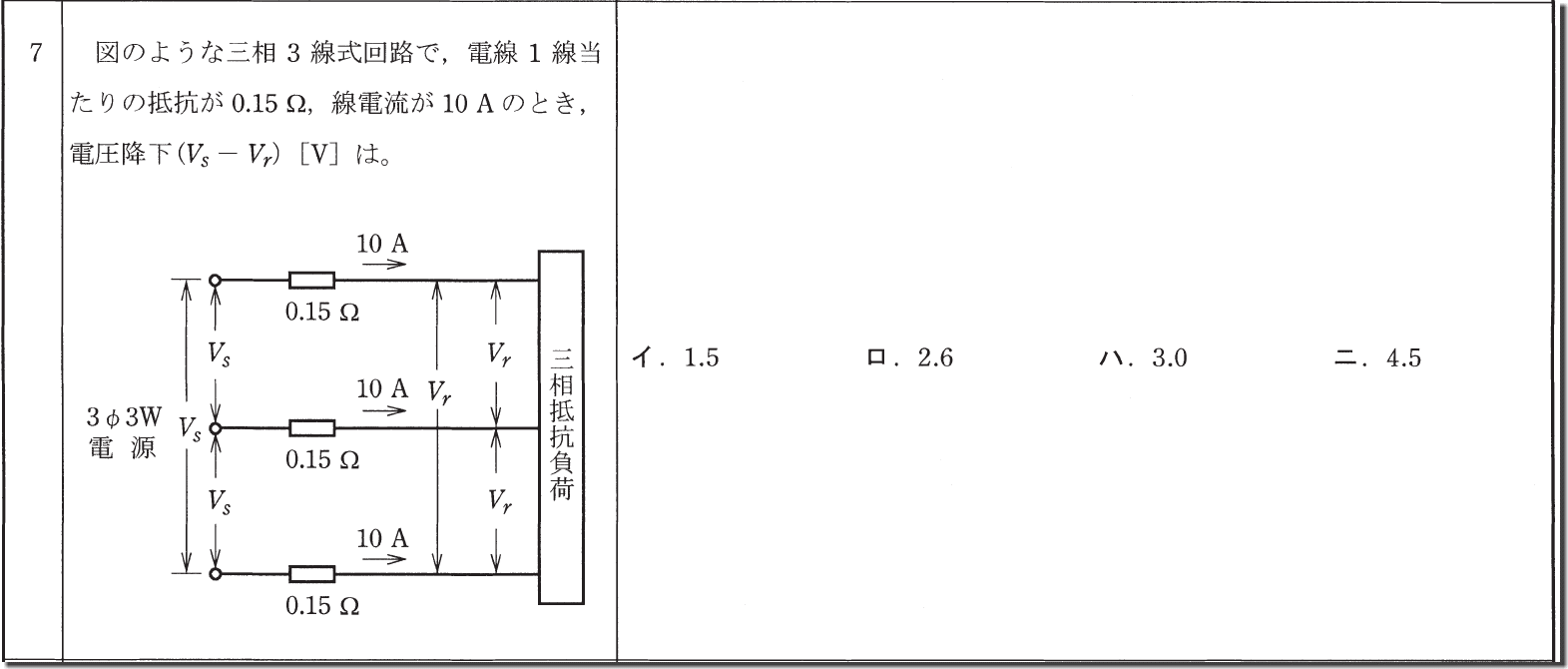
三相3線式の電圧降下は√3Irでしたが、そのまま当てはめるだけです。
√3×10×0.15→1.7×1.5
計算をする前に少し選択肢を見ると、1.5ではないですね。
次に3.0は1.5の2倍なので3.0と4.5は違いますね。
よって「ロ」の2.6が正解です。
と計算する前に答えが出ました。やったぜたえちゃん(え

ちゃんとした式でも求める事が出来ますが(参考書では主に公式での解説をしています)
が!
実はこれも、パッと見で解く事が出来る系の問題です。
まず、中央の線が断線しているという事で、そうなるとこの回路は
ただの単純な直列回路
になります。
で、ab間の抵抗は100Ωでその下は20Ωですね。
つまり、5:1になります。
全体に掛かる電圧が200Vで5:1の比率を求めるだけです。
なので、200を6等分すると大体33なのでそれの5倍で165
近いのは「ハ」の167となります。
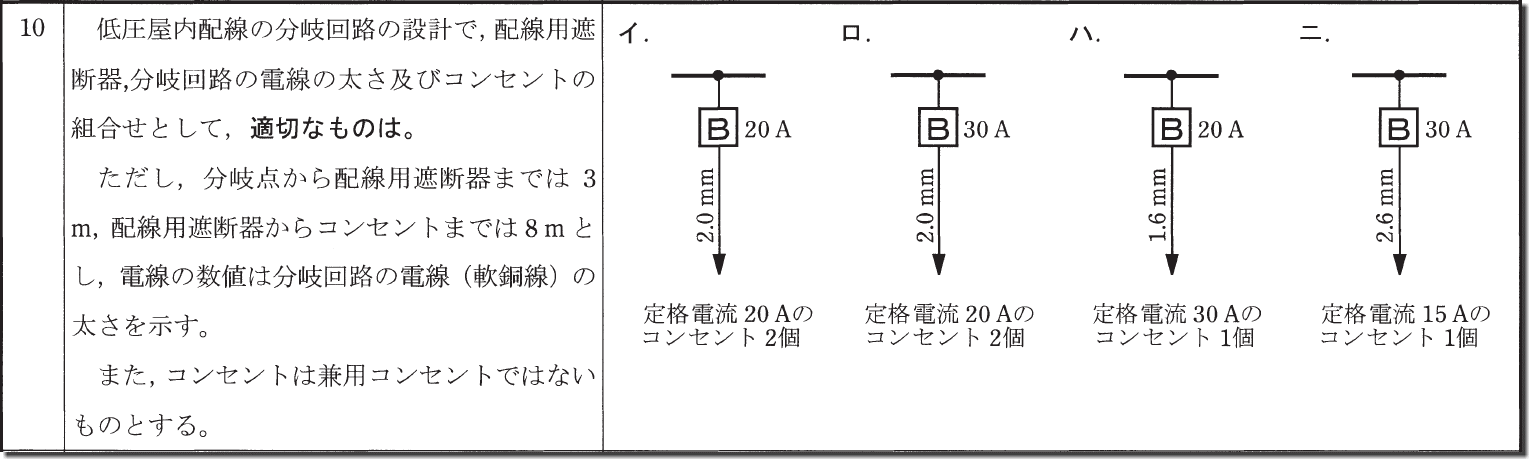
この問題はほぼ毎回出題されるのでこちらの表をしっかり暗記しておきましょう。

解説でも触れましたが、覚えるポイントはヒューズを起点に覚えるといいです。
まず、選択肢の「ハ」のように配線用遮断器よりコンセントの定格電流が大きいものは不正解です。
次に配線用遮断器が30Aの時はコンセントは20~30Aとなるので「ニ」も不正解です。
また、配線用遮断器が30Aの時は太さが2.6mm以上なので「ロ」も不正解です。
このように表をしっかり覚えておけば消去法で求める事が出来るので、しっかり暗記しましょう。
答えは「イ」です

この問題はこちらの表を使用します。

先に問題文の許容電流を確認すると34Aとあります。
これは定格電流100Aの0.34倍ですね(単純に計算して)
この0.34倍はこの表の3~8m以下と8m以上の式に全て当てはまりません。
つまり正解は「イ」の3m以下です。

この問題はこちらの表を使用します。

30Aの1.25倍が37.5Aとなりますが、
この時点で答えは「ハ」しかありません。一瞬でしたね。

この問題はこの良く分からない表を使って求めます。

まず、Ⅿを全て足したものとHを全て足したものを比較します。
M=40A、H=30A
となります。
ここでこの表を見てみると、IM>IHで40AはIM<=50なので、この表の真ん中の式を使用します。
(1.25×40)+30
この答えがそのまま答えになるので、80なので答えは「ハ」となります。
最後に
今回は計算問題に焦点を集めて解説しましたが、この電気工事士の試験ではいきなり計算問題から入るので気が滅入る事もあると思います。
しかし、実際解き方が分かると難しい計算をほとんどしなくても良い事が分かったかと思います。
他の科目も全て暗記ですが、とりあえず計算問題で6~7問正解出来れば計算問題を全て捨てるより御の字だと思います。
むしろ計算問題は稼ぎ頭だと思っているので、まずはここからしっかり勉強していきましょう。
独学で勉強する場合は、みんあ大好きすぃ~との参考書がオススメです。
良く出る問題の解説なども記載されていますが、どれもしっかりとした計算式での解説なのでしっかり理解出来ないと少し難しく感じるかもしれません。
あとは過去問をしっかり解きましょう。
市販のものでも良いですが、ネット上にも過去問は多く掲載されています。
他にも計算問題は数多くあるので、今後も他の問題の解説も随時更新していきます。
お楽しみに!!(待ってない
今回はこの辺でノシ








コメント